A geometric approach
This post discusses a way to solve part 2 of day 10 of AOC 2023. It assumes you have already done part 1 and that you know exactly which tiles are part of the loop.
Notice that the loop is a simple polygon1. Then notice that the “head” of a ray that starts outside a polygon and shoots across it will be either inside or outside the polygon at all times, depending on how many times it has crossed the polygon’s boundary2. I will apply these ideas to this problem.
Imagine a ray that starts in a place known to be outside the loop. If it never crosses the loop, then it’s never inside the loop. If it crosses the loop, now it’s inside. If it then crosses the loop again, now it’s back outside. If it then crosses the loop a third time, it’s inside again. The ray may cross the loop any number of times, but what matters is the remainder modulo 2.
Any ray suffices for this provided it doesn’t hit any vertices, because it’s ambiguous how to handle those cases. Because they’re easy, I use horizontal rays even though they do hit the loop’s vertices (i.e. corner pieces LJF7), but that means I have to think carefully about how to handle the vertex intersections. Fortunately, it’s not hard to deal with.
Given a horizontal ray, it’s obvious that hitting a ┃ counts as crossing the boundary. Meanwhile, hitting - does not count as a crossing, nor does hitting any tile that is not part of the loop. (Again, this discussion assumes you have already determined exactly which tiles are part of the loop.) What we have to think carefully about is the corner pieces. When the ray hits a L, should that count as a crossing? The fact that it’s a loop means every corner piece must be connected to another corner piece on the same row (and another one on the same column, but our ray is horizontal, so we don’t care about what’s going on far above and below us). These two corner pieces could be adjacent, but in general they’re separated by a number of horizontal tiles -. Every time the ray encounters a corner piece, there are four possible cases: L---J, L---7, F---7, F---J. Horizontal pieces don’t matter to our ray, so imagine we compress them down to nothing: LJ, L7, F7, FJ. Now consider these corner pieces as being part horizontal, part vertical. Compress out the horizontal parts of these pairs of corners, and we’re left with ╹, ┃, ╻, ┃. In other words, the ray doesn’t cross the vertical at LJ and F7, but it does at L7 and FJ.
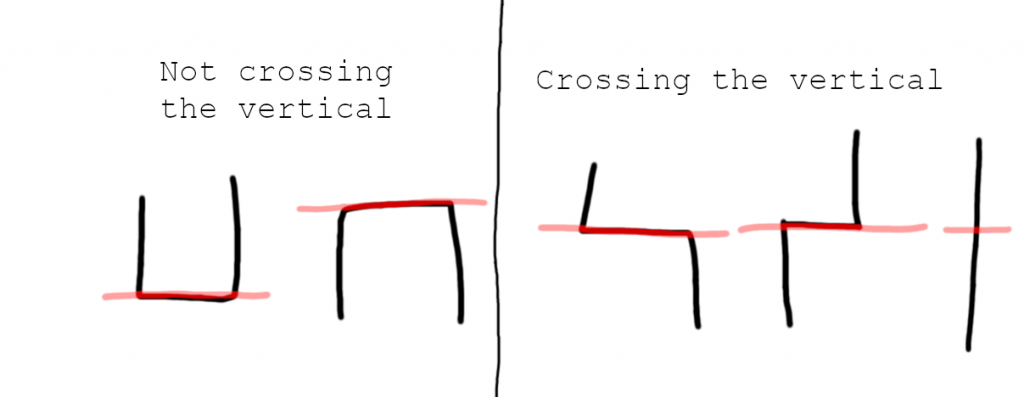
You can directly code the aforementioned logic for handling corners, and it should be easy enough. But here is a slightly different approach that I used, which led to very simple code. Imagine that instead of casting the ray perfectly in line with the center of the row, you shift it down slightly—less than a full tile height down. Now returning to think of it geometrically instead of in terms of tiles, we see that the ray never hits corners anymore! The picture becomes like this:
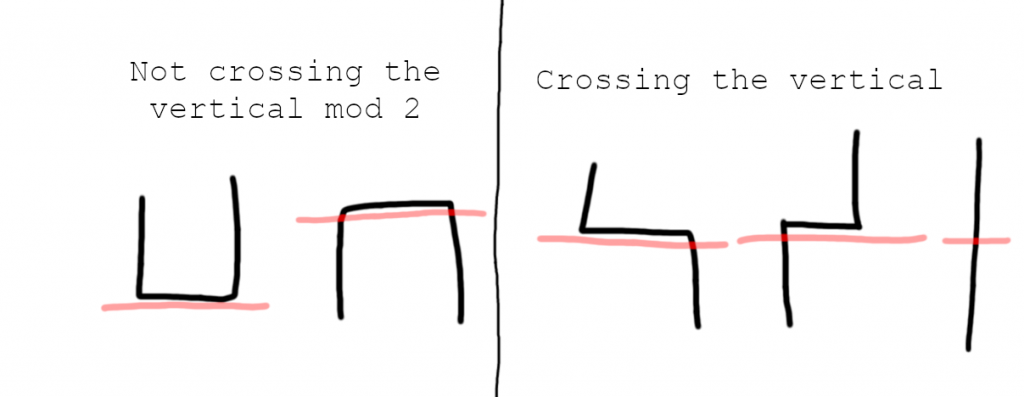
What’s the effect of this? Visually, it’s clear that LJ means 0 crossings, F7 2, L7 1, FJ 1, and ┃ 1. In By arbitrarily choosing to move the ray down and not up, this has broken the symmetry of the problem, which may seem bad. We used to treat LJ and F7 the same, but now one crosses zero times and the other crosses twice. It turns out this is fine, since crossing twice is the same as crossing zero times, per our earlier intuition about counting crossings. Meanwhile, L7 and FJ are also no longer symmetrical, as now it’s as if only the south-going 7 and F cross the ray, while the north-going L and J miss it completely. But I would justify this intuitively like this: in the non-shifted scenario, each tile in the L7 and FJ pairs counts as “half” a vertical crossing, adding up to 1—whereas after shifting down, L and F count as 0 and 7 and J as 1. The sums are preserved, which is what we care about.
Indeed, if you choose to shift the ray up instead of down (not pictured), all that will change is LJ will count as 2 crossings and F7 as 0—both still 0 mod 2, and the 1s and 0s would swap places in the analysis of L7 and FJ—both still counting as 1 crossing.
Now that we know how to count loop crossings along a ray, we can do something like cast one ray for each row in the input and simply count up the total number of inside-the-loop tiles each ray hits—which is the final answer.
Here is a sketch of my solution using the ray-shifted-down approach, sans reading the input and preprocessing it.
/* Precondition: The start tile's type reflects the connection it has to its neighbors */
/* Precondition: Every tile knows whether it is part of the loop */
var insideCount = 0;
for (var rowIdx = 0; rowIdx < rowCount; ++rowIdx) {
var inside = false;
for (var colIdx = 0; colIdx < columnCount; ++colIdx)
{
var tile = tileMap[rowIdx][colIdx];
if (tile.IsInLoop)
if (tile.Type == TileType.NorthSouth
|| tile.Type == TileType.SouthWest
|| tile.Type == TileType.SouthEast)
inside ^= true;
else if (inside)
insideCount++;
}
}
Console.WriteLine(insideCount);